علامات موازية خطوط مستقيمة

ويمكن إثبات توازي خطينوأساس النظرية، التي تنص على أن اثنين من عمودي عمودي على خط مستقيم واحد سيكون موازيا. هناك بعض علامات التوازي للخطوط - هناك ثلاثة فقط منها، وكلها سوف ننظر فيها بشكل أكثر تحديدا.

أول علامة على التوازي

خطوط مستقيمة موازية، إذا كان عند تقاطع الخط الثالث على التوالي، والزوايا الداخلية شكلت الكذب في الاتجاه المعاكس سيكون على قدم المساواة.

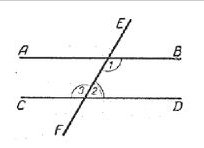
لنفترض، على عبور خطوط أب و سد من الخطبواسطة الخط إف، تم تشكيل الزوايا I1 و I2. وهي متساوية، حيث أن خط مستقيم يمر تحت منحدر واحد فيما يتعلق بالخطين الآخرين المستقيمين. عند تقاطع خطوط، وضعنا النقاط كي L - لقد حصلنا على قطعة من إف الإلكترونية. نجد وسطه ووضع نقطة O (الشكل 189).

على الخط أب نحن خفض عمودي من النقطة O. نسميها أوم. مواصلة عمودي حتى يتقاطع مع القرص المضغوط على التوالي. ونتيجة لذلك، فإن الخط الأصلي أب متعامد تماما مع من، مما يعني أن CD_ | _MN، ولكن هذا البيان يتطلب دليلا. نتيجة لخطوط عمودي وتقاطع، شكلنا مثلثين. واحد منهم هو لي، والثاني هو نوك. فلننظر فيها بمزيد من التفصيل. علامات التوازي من خطوط 7 الطبقة

هذه المثلثات متساوية لأنه، فيوفقا لشروط النظرية، / 1 = / 2، ووفقا لبناء المثلثات، الجانب أوك = الجانب أول. الزاوية مول = / نوك، لأن هذه هي زوايا عمودية. من هذا يتلو أن الجانب وزاويتين المتاخمة لها من أحد المثلثات على التوالي تساوي الجانب وزاويتين المتاخمة له، والآخر من المثلثات. وهكذا، فإن المثلث مول = تريانجلنوك، وبالتالي زاوية الكائنات الحية المحورة = زاوية كنو، ولكننا نعلم أن الكائنات الحية المحورة هو مستقيم، وبالتالي زاوية كنو المقابلة هي أيضا خط مستقيم. وهذا هو، تمكنا من إثبات أن إلى خط من، كل من خط أب، وخط مستقيم على خط سد عمودي. وهذا هو، أب و سد فيما يتعلق بعضها البعض موازية. هذا ما كنا بحاجة لإثباته. النظر في العلامات المتبقية من خطوط متوازية (الدرجة 7)، والتي تختلف عن الميزة الأولى بواسطة طريقة الإثبات.

العلامة الثانية من التوازي

وفقا للعلامة الثانية من التوازي من خطوط مستقيمة،نحن بحاجة إلى إثبات أن الزوايا التي تم الحصول عليها أثناء تقاطع خطوط متوازية أب و سد من خط إف متساوية. وهكذا، فإن علامات التوازي للخطتين المستقيمتين، الأولى والثانية، تقوم على المساواة بين الزوايا التي تم الحصول عليها عندما تتقاطع مع السطر الثالث. ونحن نفترض أن / 3 = / 2، والزاوية 1 = / 3، لأنه الرأسي لذلك. وهكذا، تكون f2 مساوية للزاوية 1، ولكن ينبغي أن تؤخذ في الاعتبار أن كلا من الزاوية 1 والزاوية 2 هما زوايا داخلية ومتداخلة. ولذلك، يبقى لنا أن نطبق معرفتنا، أي أن يكون جزأين متوازيين إذا كان الخط المتقاطع الثالث، عند تقاطعهما، الزاويتان المتشكلتان المتجاورتان متساويتان. وهكذا، وجدنا أن أب || CD.

تمكنا من إثبات أنه في ظل حالة التوازي اثنين من عمودي على خط مستقيم واحد، وفقا لنظرية المقابلة، موازية خطوط واضحة.

العلامة الثالثة من التوازي

وهناك أيضا علامة ثالثة على التوازي،والتي يتم إثباتها من خلال مجموعة من الزوايا الداخلية من جانب واحد. هذا الدليل على التوازي للخطوط يسمح لنا أن نستنتج أن اثنين من خطوط مستقيمة ستكون موازية إذا، عند تقاطع خطها الثالث على التوالي، ومجموع الزوايا الداخلية التي تم الحصول عليها من جانب واحد يساوي 2d. انظر الشكل 192.