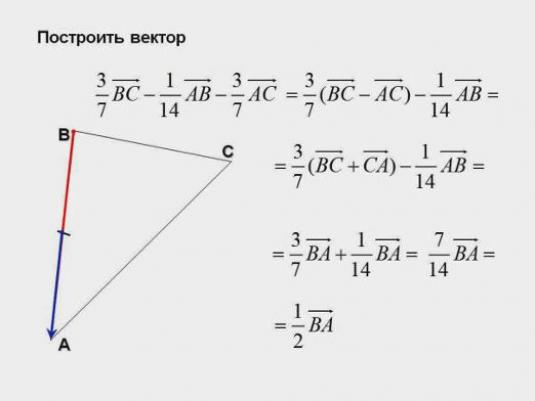
قواعد لإضافة ناقلات

من أجل تنفيذ عملية الإضافةناقلات، وهناك عدة طرق، والتي، اعتمادا على الوضع ونوع من ناقلات تعتبر، يمكن أن تكون أكثر ملاءمة للاستخدام. دعونا ننظر إلى قواعد لإضافة ناقلات:

قاعدة المثلث

قاعدة المثلث هي كما يلي: من أجل إضافة متجهين x، y من الضروري بناء متجه x بحيث يتزامن أصله مع نهاية المتجه y. ثم مجموعها ستكون قيمة المتجه z، ويتطابق أصل المتجه z مع بداية المتجه x، والنهاية بنهاية المتجه y.

قاعدة المثلث يساعد، إذا كان عدد من ناقلات التي تحتاج إلى تلخيص لا يزيد عن اثنين.

قاعدة المضلع

قاعدة المضلع هي الأبسط والأكثر ملاءمةلإضافة أي عدد من ناقلات على متن طائرة أو في الفضاء. جوهر القاعدة هو ما يلي: عند إضافة ناقلات، تحتاج إلى محاذاة متتابعة لهم واحدا تلو الآخر بحيث تتزامن بداية ناقلات لاحقة مع نهاية سابقتها، والمتجه الذي يغلق منحنى شكلت هو مجموع مصطلحات ناقلات. ويوضح ذلك بيانيا بالمعادلة w = x + y + z، حيث المتجه w هو مجموع هذه النواقل. وبالإضافة إلى ذلك، تجدر الإشارة إلى أن المبلغ لا يتغير من تغيير في أماكن من ناقلات، وهذا هو (س + ص) + ض = س + (ص + ض).

قاعدة متوازي الاضلاع

يتم استخدام قاعدة متوازي الأضلاع لإضافةناقلات التي تنشأ من نقطة واحدة. في هذه القاعدة، يقال أن مجموع المتجهات x و y، التي لها بداية عند نقطة واحدة، سيكون المتجه الثالث z المنشأ أيضا من هذه النقطة، والناقلات x و y هي جوانب متوازي الأضلاع، والناقلات z هي قطري. في هذه الحالة، فإنه لا يهم أيضا في الترتيب الذي سيتم إضافة ناقلات.

وهكذا، فإن قاعدة المضلع، قاعدة المثلث، والقاعدة متوازي الأضلاع تساعد على حل مشكلة إضافة ناقلات من أي تعقيد على الإطلاق، سواء على متن الطائرة أو في الفضاء.