ما هو متوازي؟

في الهندسة، المفاهيم الأساسية هيالطائرة، نقطة، خط وزاوية. باستخدام هذه الشروط، يمكنك وصف أي شكل هندسي. وعادة ما يتم وصف المجسمات الثلاثية الأبعاد من حيث الأشكال البسيطة التي تقع في نفس الطائرة، مثل دائرة، مثلث، مربع، مستطيل، الخ في هذه المقالة سوف نناقش ما مربع، ووصف أنواع متوازية، خصائصه، ما هي العناصر يشمل ذلك وأيضا إعطاء الصيغ الأساسية لحساب مساحة وحجم مربع لكل الأنواع.

تعريف

A متوازي في الفضاء ثلاثي الأبعاد هو المنشور، جميع جوانب منها متوازي الاضلاع. وبناء على ذلك، يمكن أن يكون ثلاثة أزواج فقط من متوازي الاضلاع المتوازي أو ستة وجوه.

لتصور مربع، تخيلتخيل الطوب القياسية. الطوب هو مثال جيد على متوازي مستطيلة، والتي حتى يمكن للطفل أن يتصور. وهناك أمثلة أخرى يمكن أن تكون بمثابة بيوت من الألواح متعددة الطوابق وخزائن وحاويات لتخزين المنتجات الغذائية ذات الشكل المناسب، وما إلى ذلك.

الأنواع من هذا الرقم

هناك نوعان فقط من متوازيات:

مستطيلة، وجميع الوجوه الجانبية التي هي في زاوية من 90^حول إلى القاعدة وهي مستطيلات.
يميل، وجوه الجانبية التي تقع في زاوية معينة إلى القاعدة.

ما العناصر التي يمكن تقسيمها إلى هذا الشكل؟

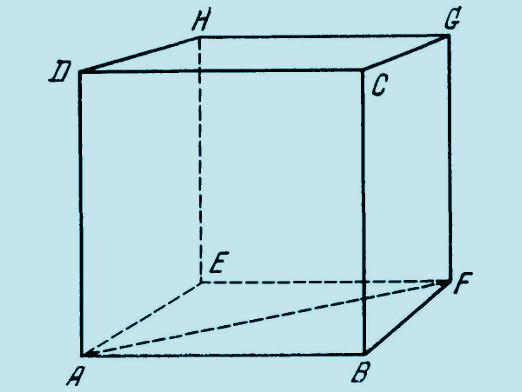
كما هو الحال في أي شكل هندسي آخر، فيمتوازية أي وجهين مع حافة مشتركة تسمى المجاورة، وتلك التي لم يكن لديك موازية (بدءا من خاصية متوازي الاضلاع وجود جانبي متوازية زوجي موازية).
وتسمى القمم المتوازية التي لا تكذب على وجه واحد عكس ذلك.
الجزء الذي يربط هذه القمم هو قطري.
إن أطوال الحواف الثلاثة المتوازية المستطيلة التي تنضم إلى قمة واحدة هي أبعادها (أي طولها وعرضها وطولها).

خصائص الشكل

هو دائما بنيت بشكل متناظر فيما يتعلق إلى منتصف قطري.
نقطة تقاطع كل الأقطار يقسم كل قطري إلى قسمين متساويين.
وتكون الوجوه المقابلة متساوية الطول وتستقر على خطوط مستقيمة متوازية.
إذا قمت بدمج مربعات جميع أبعاد المربع، فإن القيمة الناتجة تكون مساوية لمربع طول قطري.

الصيغ الحساب

الصيغ لكل حالة معينة من متوازي سيكون لها خاصة بهم.

ل متوازي التعسفي صحيحوالتأكيد على أن حجمه يساوي القيمة المطلقة للمنتج الثلاثي العددية من ناقلات من ثلاثة جوانب المنبثقة عن قمة واحدة. ومع ذلك، لا توجد صيغة لحساب حجم موازية التعسفي.

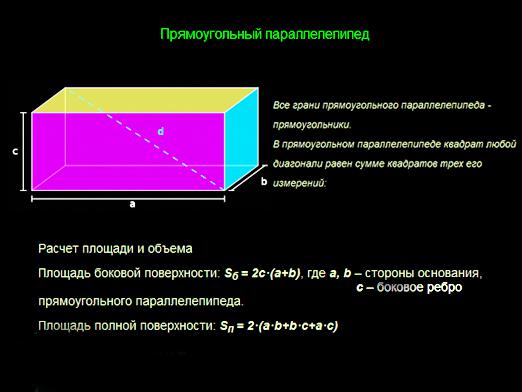
بالنسبة لمعادلة متوازية مستطيلة، تطبق الصيغ التالية:

V = a * b * c؛
سب = 2 * c * (a + b)؛
سن = 2 * (a * b + b * c + a * c).

حيث:

V هو حجم هذا الرقم.
سب هو مساحة السطح الجانبي.
سن هو إجمالي مساحة السطح.
a هو طول؛
b هو العرض؛
ج - الارتفاع.

حالة خاصة أخرى من متوازي، فيالتي جميع الأطراف هي الساحات، هو المكعب. إذا كان يرمز إلى أي من جانبي الساحة بالحرف a، ثم بالنسبة لمساحة السطح وحجم الرقم المعطى، يمكن استخدام الصيغ التالية:

S = 6 * a * 2؛
V = 3 * a.

حيث:

S هو مجال هذا الرقم،
V هو حجم هذا الرقم،
a هو طول وجه هذا الرقم.

آخر مجموعة ننظر فيهاومتوازي هو مستقيم متوازي. ما هو الفرق بين متوازية مستقيمة ومستطيلة متوازي، تسأل. حقيقة أن أساس متوازي المستطيلات يمكن أن يكون أي متوازي الاضلاع، وأساس مباشرة - مجرد مستطيل. إذا كنا دلالة على محيط قاعدة تساوي مجموع أطوال من جميع الجهات، كما بو، وارتفاع يرمز له بالحرف ساعة، قد نستخدم الصيغة التالية لحساب حجم ومساحة المجموع والأسطح الجانبية: